前一篇我们已经将隐变量的先验概率,隐变量的后验概率,和样本的联合概率都表示出来了,这一节我们来详细看一下EM算法。
2.1 最大似然
假设现在的数据集表示为,则我们可以用一个矩阵来表示这个数据集。假设每个数据的维度是维的,那么我们可以把矩阵的每一行表示为数据集中的一条数据,矩阵就一共有行矩阵,这样这个矩阵的规模就是的。我们再把隐变量也这样表示出来,每个数据对应一条隐变量,假设隐变量的长度是,那么隐变量矩阵的规模就是。
作为一个生成模型,我们可以把高斯混合模型的概率图表示出来:
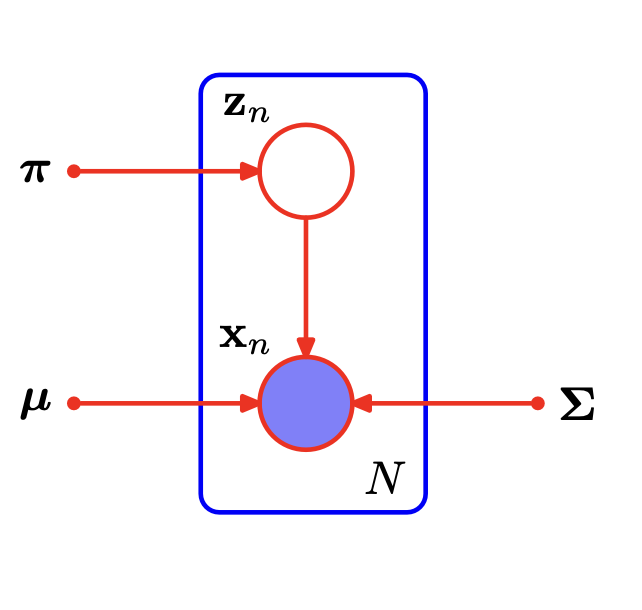
来源:Pattern Recognition and Machine Learning P433 表示个独立同分布的数据点,对应隐变量的高斯混合模型概率图
这也是最简单的概率图模型。
根据上一节我们推导出的高斯混合模型公式,我们可以写出对数似然函数
关于这个对数似然函数的奇异性的讨论不做过多介绍,主要讲推导。
2.2 用于高斯混合模型的EM
对似然函数的均值求偏导,可以得到
若似然函数取最大值,则必有偏导数为0,令上式等于0,再尝试整理公式使得将移动到等式左边,同时两边乘可以得到
其中
可以将理解为聚类的数据点的有效数量。因为可以看成是某个高斯分布,指的是某条数据,这个式子就是将每条数据对于第k个高斯分布的贡献值或者说是责任值之和就是对于的有效数量。那么公式(3)就可以理解成就是一个加权平均。并且,相当于将每一项的责任值加了起来。
同理可以求的偏导数,得
上面两式子存在一个约束条件,就是的和必须为1,这点我们在上一篇文章已经讲过,所以对于,我们需要使用拉格朗日乘数法来进行计算:
代入本篇的(1)式,可以得到
(7)式的第一项相比于(2)少了一个,等式两边同时乘,可以得到
从1到进行积分,可以得到
将结论带入到(7),可以得到
我们得到了第k个分量的"混合系数",或者说是责任平均值。
求出来之后,我们就可以来说一下EM算法的过程:
初始化,计算对数似然函数(对应本片中的公式(1))的初始值。
E步骤。计算当前参数值的"责任":
M步骤,重新计算参数:
其中:
检查参数或者新的对数似然函数是否收敛,若收敛则结束,否则使用新的参数并返回第2步。
高斯混合模型的EM算法步骤如上所述。

